Next: 6.3 田辺 Up: 6. Hilbert 変換 Previous: 6.1 数直線上の Hilbert 変換
数直線上定義された関数 ![]() ,
, 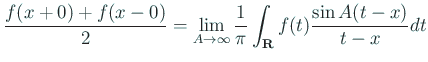 が、次のいずれかの条件を満足す
るとする:
が、次のいずれかの条件を満足す
るとする:
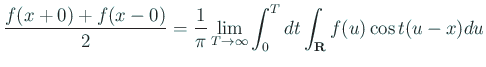
| (6.5) |
また ![]() で
で ![]() が有界変動である時、
Fourier の 2 重積分定理 (double integral theorem of Fourier)
が有界変動である時、
Fourier の 2 重積分定理 (double integral theorem of Fourier)
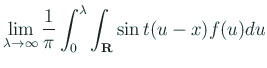 という形をとり、
という形をとり、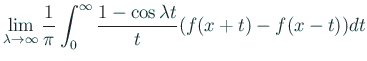 が単調に 0
に収束する。
が単調に 0
に収束する。
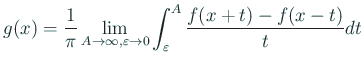
を (6.6) の右辺の積分の共役 Fourier 積分 と呼ぶ。これは形式的に
| (6.7) |
| (6.8) |
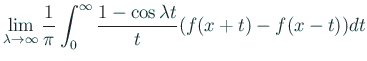 は
は | (6.9) | 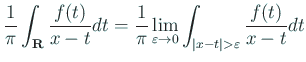 |
桂田 祐史