3.2 Banach 空間の部分集合の直交について

(閉値域の定理の準備として命題を寄せ集めたが、現在は「不要」な内容)

$\begin{jdefinition}[直交] ノルム空間 $X$\ の部分集合 $M$\ に対し... ...n X;\forall f\in L\ \langle f,x\rangle =0\}. \end{displaymath}\end{jdefinition}$

$M^\perp$ はの、 ${}^\perp L$ はの、ともに閉線型部分空間である。

$\begin{jproposition} $X$\ をノルム空間、$M$\ を $X$\ の線型部分空... ...th} ({}^\perp N)^\perp \supset \overline N. \end{displaymath}\end{jproposition}$

次の命題が成り立つ (藤田・黒田・伊藤 [7] の補題 9.8)。

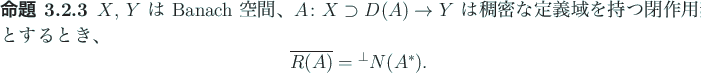
$\begin{jproposition} $X$, $Y$\ は Banach 空間、 $A\colon X\supset D(A)\to Y... ...aymath} \overline{R(A)}={}^\perp N(A^\ast). \end{displaymath}\end{jproposition}$

以下の3つの命題は田辺 [6] から引用した。

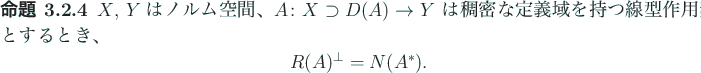
$\begin{jproposition} $X$, $Y$はノルム空間、 $A\colon X\supset D(A)\to Y$... ...� \begin{displaymath} R(A)^\perp=N(A^\ast). \end{displaymath}\end{jproposition}$

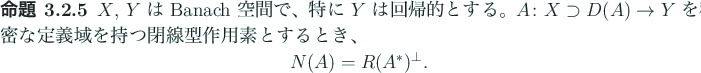
$\begin{jproposition} $X$, $Y$\ は Banach 空間で、特に $Y$\ は回帰的... ...� \begin{displaymath} N(A)=R(A^\ast)^\perp. \end{displaymath}\end{jproposition}$

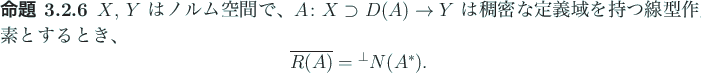
$\begin{jproposition} $X$, $Y$\ はノルム空間で、 $A\colon X\supset D(A)\... ...aymath} \overline{R(A)}={}^\perp N(A^\ast). \end{displaymath}\end{jproposition}$

はて？命題 3.2.6 は命題 3.2.3 よりも明らかに強い。実は、田辺 [6] には命題 3.2.6 の証明は載っていないが、命題 3.2.4 を認めれば (これは証明が載っている)、両辺の直交を取って、 ${}^\perp(V^\perp)=\overline V$ を用いれば (これは一般に成り立つと思っているのだが) 明らかそうだが。 (何か、あまり整理されていない印象がある…)

Brezis [10] には次の定理が載っている。

$\begin{jproposition} $X$, $Y$\ は Banach 空間で、 $A\colon X\supset D(A)\t... ...) \item ${}^\perp N(A^\ast)=\overline{R(A)}$. \end{enumerate}\end{jproposition}$

桂田祐史
2017-04-30