Next: 3.2 Banach 空間の部分集合の直交について Up: 3.1 位相的直和、位相的補空間についてぶつぶつ Previous: 3.1.2.2 テキストに見られる二つの流儀
この項の内容は主に Brezis [10] による。 なお、[10] では代数的直和を単に「直和」と書いているが、 この文書では誤解のないようにつねに「代数的直和」と書く。
Hilbert 空間 ![]() では、
任意の閉線型部分空間
では、
任意の閉線型部分空間 ![]() について
について
が成立する。
この一般化、つまり内積を考えない直和分解を考えよう。
![]() が二つの線型部分空間
が二つの線型部分空間 ![]() と
と ![]() の代数的直和であるとは、
の代数的直和であるとは、
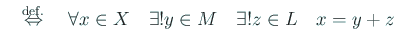
ということであった (
有限次元線型空間のことを思い出しても、
![]() の相手「補空間」
の相手「補空間」 ![]() は一意的には決まらない、
ということをまず注意しておく。
は一意的には決まらない、
ということをまず注意しておく。
無限次元空間の場合は、位相的なことを考慮する必要がある。
一言で言うと、![]() と
と ![]() を閉集合であるという条件を付加する。
こうしておくとそれぞれへの射影作用素が連続になる
(以下の系 3.1.11 を参照)。
を閉集合であるという条件を付加する。
こうしておくとそれぞれへの射影作用素が連続になる
(以下の系 3.1.11 を参照)。
![\begin{jdefinition}[位相的補空間]
$X$\ は Banach 空間で、
$M$\ を $...
...��閉集合。
\item $M\cap L=\{0\}$, $M+L=X$.
\end{enumerate}\end{jdefinition}](img142.gif)
|
この定義の状況下で、
![]() から
から ![]() や
や ![]() への射影は連続になる (以下で証明する)。
への射影は連続になる (以下で証明する)。
明らかに、
Hilbert 空間においては、
任意の閉線型部分空間 ![]() に対して、
に対して、
![]() の直交補空間
の直交補空間 ![]() は
は ![]() の位相的補空間になっている。
の位相的補空間になっている。
![\begin{jproposition}[Brezis \cite{Brezis} 命題II.8]
$X$\ を Banach 空間、...
...ox{and}\quad
\Vert z\Vert\le C\Vert x\Vert.
\end{displaymath}\end{jproposition}](img144.gif)
|
証明
![]() にノルム
にノルム
![]() を
与えたノルム空間と、
を
与えたノルム空間と、
![]() の部分ノルム空間
の部分ノルム空間 ![]() を考え、
を考え、
![]() を
を
で定めると、これは有界線型かつ全射であるから、 開写像定理により、
これから任意の
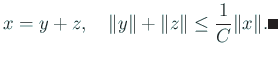
この補題から次の系は明らかである。
![\begin{jcorollary}[位相的直和において射影は連続]
を参照)。
$X...
...$x=y+z$) はともに連続かつ線型な作用素である。
\end{jcorollary}](img158.gif)
|
ところで、ここが重要なことだが、
任意に選んだ閉線型部分空間 ![]() に対して、
その位相的補空間が存在するとは限らない。
に対して、
その位相的補空間が存在するとは限らない。
![\begin{jproposition}[位相的補空間の存在・否存在]
\begin{enumerate}[...
...��間を持つ (Lindenstrauss and Tzafriri)。
\end{enumerate}\end{jproposition}](img159.gif)
|
(証明はとりあえず省略。 (1), (2) については例えば Brezis [10] などを見よ。 小松・伊藤 [3] や Treves [11] にもあったかな。 (3) については、Banach に載っているとも。)
![]() のときの
のときの
![]() や
や ![]() においても、
位相的射影を持たない閉線型部分空間がある。
これらが Hilbert 空間と同型でないことを示せば良いわけだが、
においても、
位相的射影を持たない閉線型部分空間がある。
これらが Hilbert 空間と同型でないことを示せば良いわけだが、
F.J.Murray, Trans.Amer.Math.Soc. 41 (1937), 138-152にあるとか (岡本・中村 [3] に載っていた情報)。
桂田 祐史