3.2 Givens 変換

$p$ , $q\in\{1,\cdots,n\}$ , $p\ne q$ , $\theta\in\R$ とするとき、 「$x_p x_q$ 平面における $-\theta$ の回転」を表わす行列 $G=G(p,q,\theta)=(g_{ij})$ を

$$g_{ij}= \left\{ \begin{array}{ll} \cos\theta & \mbox{($i=j\in\... ...& \mbox{($i=j\not\in\{p,q\}$)}\\ 0 & \mbox{(その他)} \end{array} \right.$$

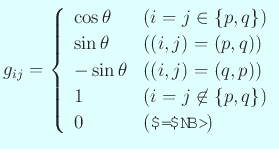
で定義する。これは明らかに実直交行列である。

Givens 変換の行列

   1 % Givens.m
   2 %  G(p,q,θ)∈M(n;R) (p≠q, c=cosθ, s=sinθ)
   3 function G = Givens(n,p,q,c,s)
   4   G = eye(n,n);
   5   G(p,p) =   c; G(p,q) = s;
   6   G(q,p) = - s; G(q,q) = c;