



Next: 6.5.0.4 素朴な疑問をぶつぶつと
Up: 6.5 都合が「よくない」場合の Lanczos 法
Previous: 6.5.0.2 うまく を取ると となる場合であっても
ここでは 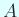 の最小多項式の問題には触れないことにする。
最初に選んだ
の最小多項式の問題には触れないことにする。
最初に選んだ  に対して
に対して
 と仮定する。
と仮定する。
 とおくと、
とおくと、
 である。
である。
 のことを単に
のことを単に
 と書くことにする。
と書くことにする。
明らかに
 は
は 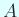 不変、すなわち
不変、すなわち
をみたすが、
 の直交補空間
の直交補空間
も 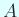 不変である。実際
不変である。実際
 とするとき、
任意の
とするとき、
任意の
 に対して、
に対して、
がなりたつので
 となり、
となり、
 が
が
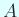 不変であることが分かる。
不変であることが分かる。
老婆心:
 とするとき、
任意の
とするとき、
任意の  に対して
に対して
 であるから、
であるから、
 .
.
そこで最初に選んだ  に対して、
に対して、
 であった場合は、
まず
であった場合は、
まず
 の正規直交基底を取り、
その後で
の正規直交基底を取り、
その後で
 ,
,  から始めて、
から始めて、
 の正規直交基底を取り、
以下この操作を続けていけば、最後には
の正規直交基底を取り、
以下この操作を続けていけば、最後には
とできる。
それと並行して、
 の正規直交基底
の正規直交基底
 (
(
 ) が得られる。
この正規直交基底を
) が得られる。
この正規直交基底を
と並べたものを
 として、
として、
 とおくと、
とおくと、
こうして得られた  は確かに三重対角行列である。
は確かに三重対角行列である。





Next: 6.5.0.4 素朴な疑問をぶつぶつと
Up: 6.5 都合が「よくない」場合の Lanczos 法
Previous: 6.5.0.2 うまく を取ると となる場合であっても
桂田 祐史
2015-12-22
![]() は
は ![]() 不変、すなわち
不変、すなわち
![]() とするとき、
任意の
とするとき、
任意の ![]() に対して
に対して
![]() であるから、
であるから、
![]() .
.
![]() に対して、
に対して、
![]() であった場合は、
まず
であった場合は、
まず
![]() の正規直交基底を取り、
その後で
の正規直交基底を取り、
その後で
![]() ,
, ![]() から始めて、
から始めて、
![]() の正規直交基底を取り、
以下この操作を続けていけば、最後には
の正規直交基底を取り、
以下この操作を続けていけば、最後には

![]() は確かに三重対角行列である。
は確かに三重対角行列である。
