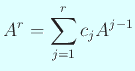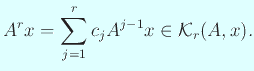Next: 6.5.0.2 うまく を取ると となる場合であっても
Up: 6.5 都合が「よくない」場合の Lanczos 法
Previous: 6.5 都合が「よくない」場合の Lanczos 法
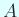 の最小多項式
の最小多項式
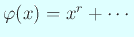 の次数
の次数  が
が  より小さい場合は、
より小さい場合は、
をみたす 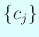 が存在する。すると任意の
が存在する。すると任意の  に対して
に対して
したがって
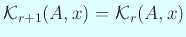 . ゆえに
. ゆえに
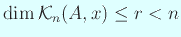 となる。
従って
となる。
従って
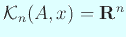 をみたす
をみたす 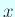 は存在しない。
は存在しない。




Next: 6.5.0.2 うまく を取ると となる場合であっても
Up: 6.5 都合が「よくない」場合の Lanczos 法
Previous: 6.5 都合が「よくない」場合の Lanczos 法
桂田 祐史
2015-12-22