Next: 1.3 ТюЅжЎљТгАтЁЃуЅѕ Fredholm сЂ«т«џуљє Up: 1. Fredholm сЂ«ТіъСИђт«џуљєсЂ«ТюЅжЎљТгАтЁЃсЃљсЃ╝сѓИсЃДсЃ│ Previous: 1.1.3 Riesz-Schauder уљєУФќ, Fredholm
![]() сѓњ
сѓњ ![]() сЂЙсЂЪсЂ»
сЂЙсЂЪсЂ» ![]() сѓњУАесЂЎсѓѓсЂ«сЂесЂЎсѓІсђѓ
сѓњУАесЂЎсѓѓсЂ«сЂесЂЎсѓІсђѓ
![]() сЂесЂЎсѓІсђѓ
сѓѓсЂАсѓЇсѓЊ
сЂесЂЎсѓІсђѓ
сѓѓсЂАсѓЇсѓЊ
![]() сЂДсЂѓсѓісђЂ
сЂДсЂѓсѓісђЂ
![]() сЂДсЂѓсѓІсђѓ
сЂДсЂѓсѓІсђѓ
сЂФсѓѕсЂБсЂдсђЂ
|
|
Уе╝Тўј
жђєсЂФсЂЊсЂ«ТђДУ│фсЂД
|
|
Уе╝Тўј
![]() сЂесЂЎсѓІсЂесЂЇсђЂ
сЂесЂЎсѓІсЂесЂЇсђЂ
|
|
Уе╝Тўј
![]() сЂФТ│еТёЈсЂЎсѓїсЂ░сѓѕсЂёсђѓ
сЂФТ│еТёЈсЂЎсѓїсЂ░сѓѕсЂёсђѓ ![]()
![]()
уиџтйбС╗БТЋ░сЂ«тИИУГў1.1
сЂ»
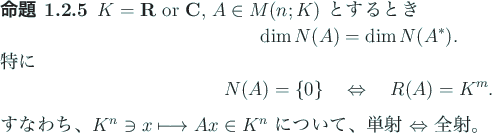
|

ТАѓућ░ уЦљтЈ▓