Next: 7.3 埋め込まれた空間の双対 Up: 7. 双対空間についてのメモ Previous: 7.1 埋め込み写像
(この節は読みやすさは別にして十分整理できている。)
![]() または
または ![]() とし、
とし、
![]() を
を ![]() 上の内積空間 (pre-Hilbert 空間)、
上の内積空間 (pre-Hilbert 空間)、
![]() をその内積とする。
をその内積とする。
![]() の双対空間
の双対空間 ![]() は (位相線形空間の一般論に従って)
は (位相線形空間の一般論に従って)
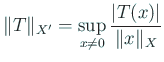
として定義されるが、今の場合
をノルムに持つノルム空間であるから、
というノルムにより Banach 空間になる。
![]() に対して、
に対して、
で定義される
という有界性の条件が得られて証明できる。これから
![]() という写像を
という写像を ![]() で表す。つまり
で表す。つまり
![]() は
は ![]() のとき線型、
のとき線型、![]() のとき共役線型となる。すなわち、
のとき共役線型となる。すなわち、
(7.1) から ![]() は等長写像 (
は等長写像 (
 ) であるから、
) であるから、

となるので、
ここまでをまとめておこう。
![\begin{jlemma}[内積空間からその双対空間への標準的な単射]
$K...
...役線型な等長写像 (ゆえに連続かつ単射) である。
\end{jlemma}](img384.gif)
|
![]() が Hilbert 空間である場合は、
が Hilbert 空間である場合は、![]() は全射になる。
すなわち次の定理が成り立つ。
は全射になる。
すなわち次の定理が成り立つ。
|
|
![\begin{jcorollary}[Hilbert 空間の共役空間は Hilbert 空間]
$X$\ を Hi...
...
\end{displaymath}を内積とする Hilbert 空間となる。
\end{jcorollary}](img386.gif)
|
特に ![]() が実 Hilbert 空間のとき、
が実 Hilbert 空間のとき、
![]() は Hilbert 空間の同型写像である。
は Hilbert 空間の同型写像である。
Riesz の定理から Hilbert 空間は反射的であることも示せる (ここでは証明略)。
次の命題もよく使われる。
|
|
証明
任意に ![]() を固定するとき、
を固定するとき、
![]() は
は ![]() 上の連続線型形式である。
これを
上の連続線型形式である。
これを ![]() と書くと、
と書くと、
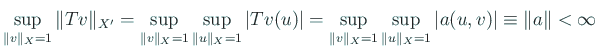 という写像が定義できるが、
という写像が定義できるが、
![]() は明らかに共役線型である。また
は明らかに共役線型である。また
であるから、
 は二つの有界共役線型作用素の積であるから有界線型作用素であり、
は二つの有界共役線型作用素の積であるから有界線型作用素であり、
となる。
|
|
証明
![]() とすると、
とすると、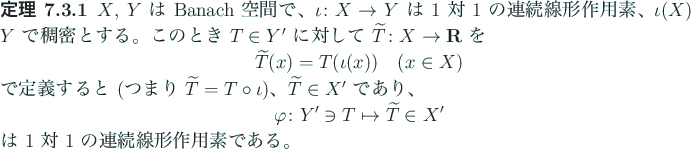 は
有界準双線型形式になるので、
上の命題を適用して、
は
有界準双線型形式になるので、
上の命題を適用して、
![]() を
満たす有界線型作用素
を
満たす有界線型作用素 ![]() が存在する。
が存在する。 ![]()
桂田 祐史