


Next: B..2 ユークリッドの互除法による Strum 列の生成
Up: B..1 スツルムの定理
Previous: B..1.0.1 (1) の証明
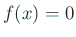 の解
の解  において考える。Strum 列の条件 (4) は
において考える。Strum 列の条件 (4) は  と
と
 が同符号であることを示している。例えば
が同符号であることを示している。例えば  の場合、
十分小さな
の場合、
十分小さな  を取ると、
これから
を取ると、
これから
であることが分かる。 の場合も同様の議論で
の場合も同様の議論で
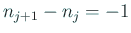 であることが分かる。
であることが分かる。



Next: B..2 ユークリッドの互除法による Strum 列の生成
Up: B..1 スツルムの定理
Previous: B..1.0.1 (1) の証明
桂田 祐史
2015-12-22