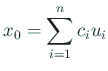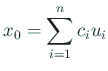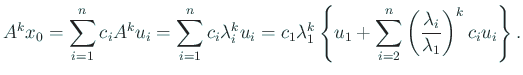


Next: 2.4 固有ベクトルから固有値を求める方法
Up: 2.3 巾乗法(power method)
Previous: 2.3 巾乗法(power method)
まず適当な 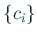 を選ぶことにより
を選ぶことにより
と展開されることに注意する。ここで 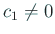 である。
である。
ここで
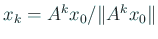 であることに注意すると、
であることに注意すると、
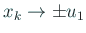 (
(
 ) となることが分かる。
) となることが分かる。



Next: 2.4 固有ベクトルから固有値を求める方法
Up: 2.3 巾乗法(power method)
Previous: 2.3 巾乗法(power method)
桂田 祐史
2015-12-22