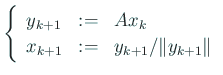


Next: 2.3.0.1 大雑把な説明
Up: 2 解法についての概観
Previous: 2.2 Jacobi 法
ここでも問題は対称であると仮定する。
与えられた行列の絶対値最大の固有値を求めるための、累乗法あるいは巾乗
法2を説明する。
行列 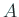 の固有値
の固有値
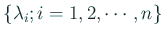 は絶対値の順に番号
づけられているとする:
は絶対値の順に番号
づけられているとする:
また、
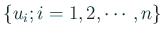 は
は
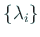 に対応する
に対応する 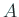 の固
有ベクトルからなる正規直交基底とする。
の固
有ベクトルからなる正規直交基底とする。
ここで話を簡単にするために次の仮定をおく。
仮定:

.
 (
(
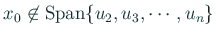 ) を選んで
) を選んで
によりベクトル列
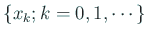 を定めると、
を定めると、
となる。実際には十分大きな番号 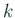 を取れば、
を取れば、
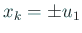 とみなして
よい。
とみなして
よい。
Subsections



Next: 2.3.0.1 大雑把な説明
Up: 2 解法についての概観
Previous: 2.2 Jacobi 法
桂田 祐史
2015-12-22
![]() の固有値
の固有値
![]() は絶対値の順に番号
づけられているとする:
は絶対値の順に番号
づけられているとする: