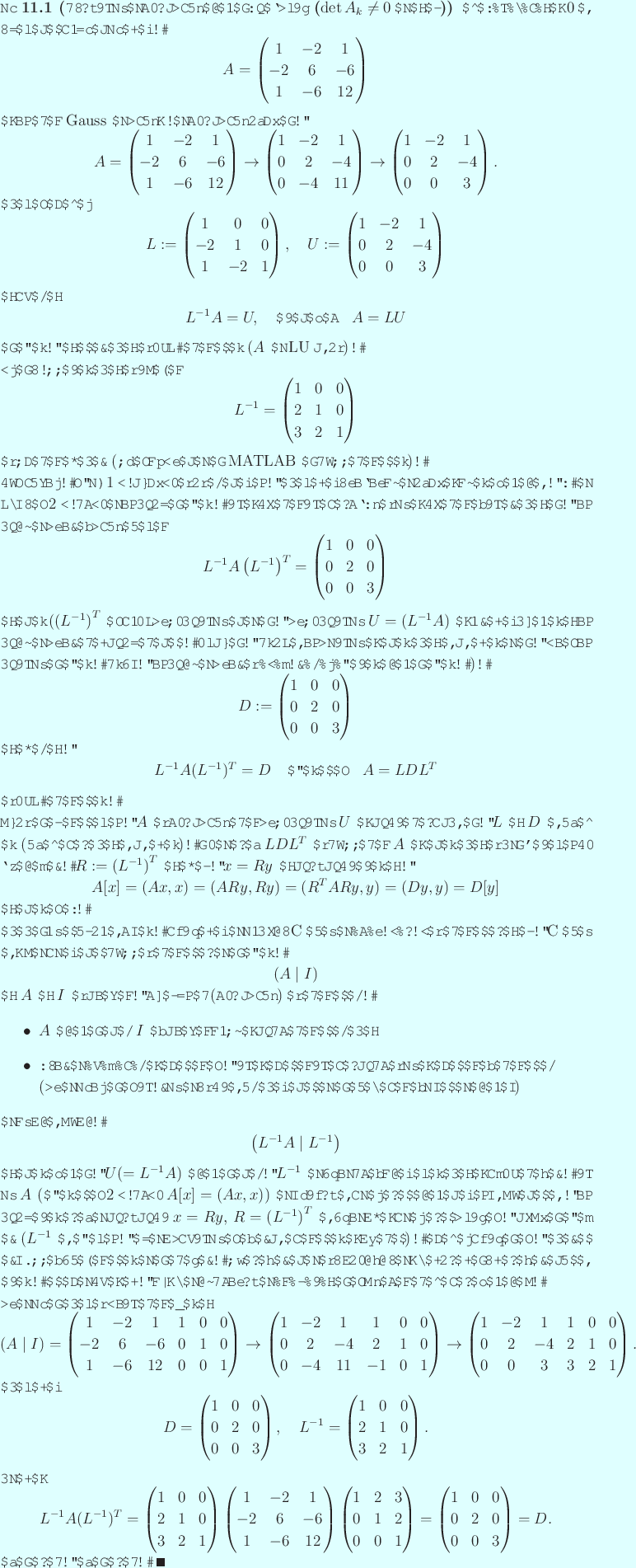
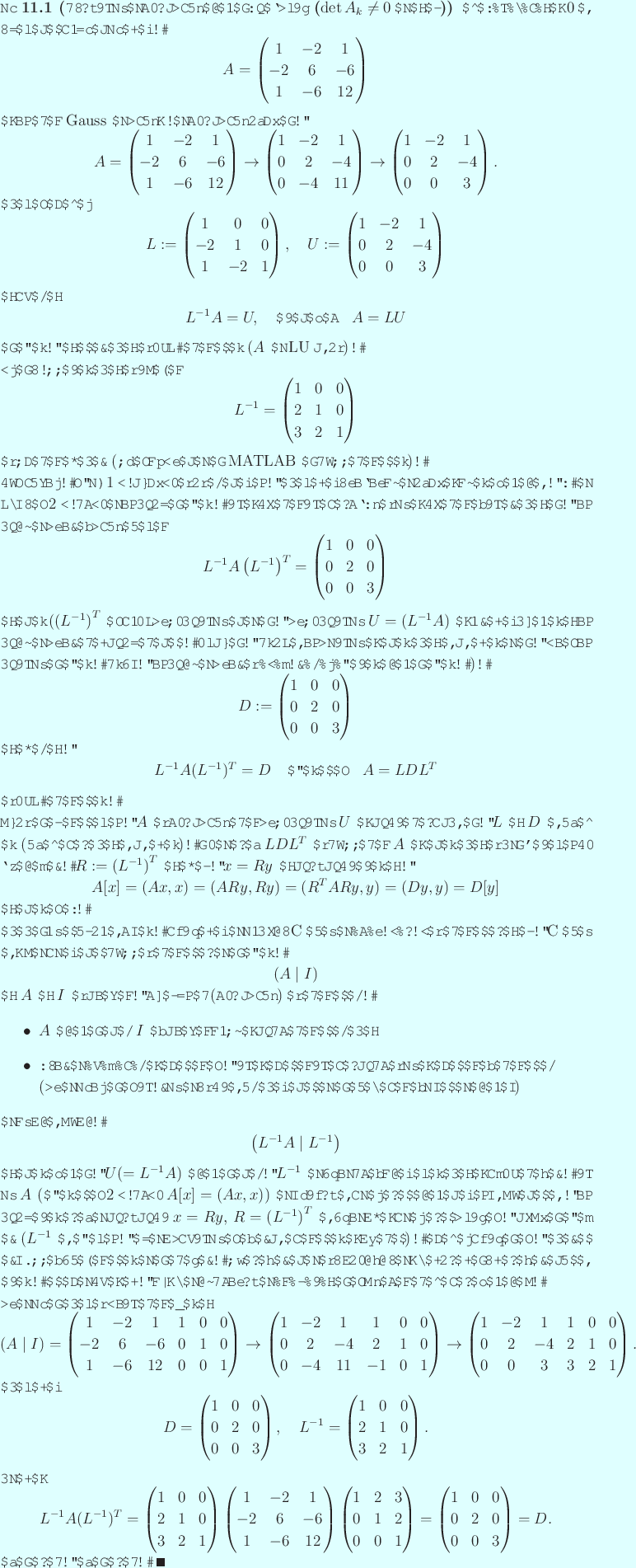
![\begin{jexample}[楽屋裏の紹介と例の追加]
上の例は逆算して作...
...\\
0&-2& 0\\
0& 0& 3
\end{pmatrix} =D. \qed
\end{displaymath}\end{jexample}](img604.png)

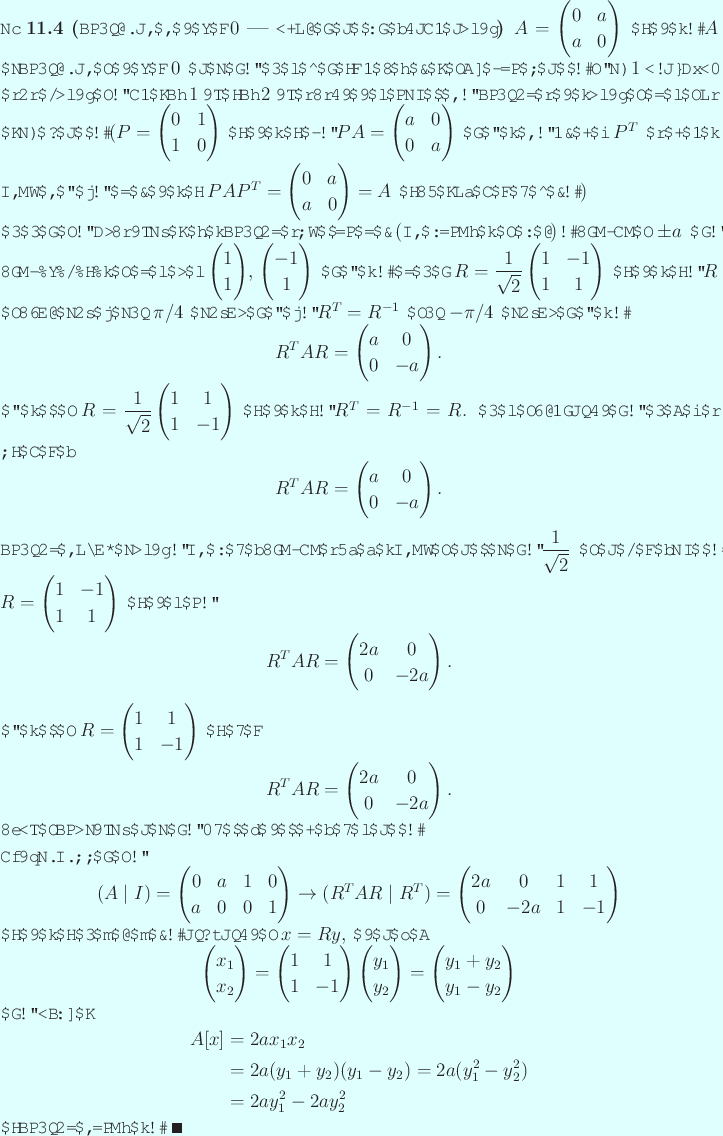
なお、
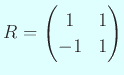
の逆行列は
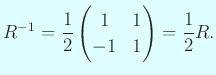
上の例は簡単であるが、 一般の場合に基本操作として使うことが出来る。 それを説明しよう。
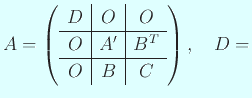 対角行列
対角行列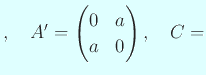 対称行列
対称行列
とする (つまり掃き出しの過程で対角成分が 0 のブロックが出て来た場合を考える)。
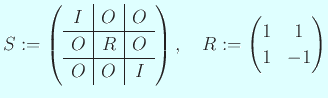
とすると、
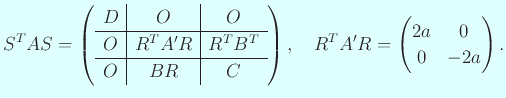
ピボットが見つからないという障害物を突破できた。
すなわち
|
( |
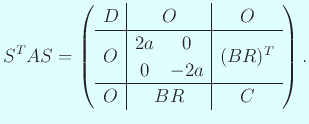 |
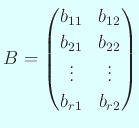 とするとき
とするとき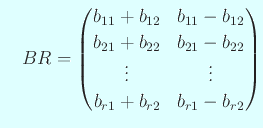
であることを注意しておく。
(![]() ) の形になれば、
2段階の掃き出しが出来て
) の形になれば、
2段階の掃き出しが出来て
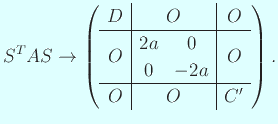
少し脇道にそれるが、後のために注意しておくと
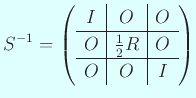
である。

より一般の場合、すなわち
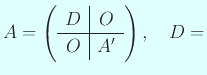
で、
found = 0;
for (i=k; i<=n; i++) {
for (j=k; j<=n; j++) { // j=i+1 からで良いのかな?
if (a[i][j] != 0) {
found = 1;
break;
}
}
}
|
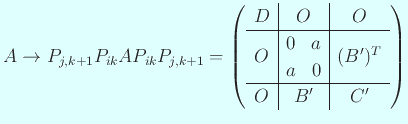
の形になる。 ここで