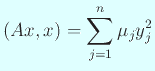Next: 11.4 2次形式の対角化のアルゴリズム (後でどこかで使うもの)
Up: 11.3 Sylvester の慣性律の証明
Previous: 11.3.0.1 定理11.1 の証明
 を
を  次実対称行列とする。
次実対称行列とする。
とおく。
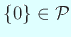 ,
, 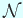 ,
, 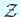 であるから、
であるから、
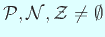 .
.
が定まる (念のため:
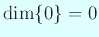 である)。
である)。
主張:
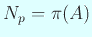 ,
,
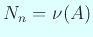 ,
,
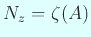 .
.
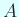 は実対称行列であるから、
固有ベクトルからなる正規直交基底
は実対称行列であるから、
固有ベクトルからなる正規直交基底
 が存在する。
が存在する。
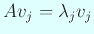 として、
として、
とおくと、
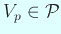 ,
,
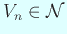 ,
,
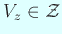 .
.
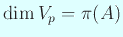 ,
,
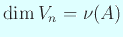 ,
,
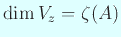 であるから、
であるから、
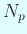 ,
, 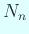 ,
, 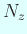 の最大性によって
の最大性によって
( )
) |
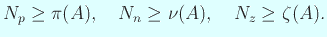 |
さて、一般に
が成り立つことは容易に証明できる。
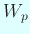 ,
, 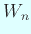 ,
, 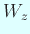 として、特に
として、特に
を満たすものを取って、
において、次元を調べる。(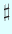 ) を用いると
) を用いると
左辺と右辺が一致するので、不等式はすべて等式で
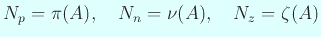
(主張の証明終わり)

さて、正則行列 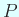 による変換
による変換 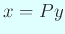 で、
で、
になったとする。簡単のために順番を修正して、
最初の  個は正,次の
個は正,次の  個は負、残りは 0
, と出来る。つまり
個は負、残りは 0
, と出来る。つまり
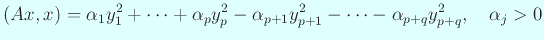
(
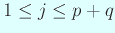
)
として良い。
- (a)
 次元空間
次元空間
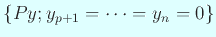 では
では 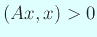 になるので、
になるので、
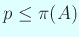 .
.
- (b)
 次元空間
次元空間
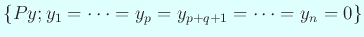 では
では 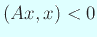 になるので、
になるので、
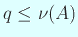 .
.
- (c)
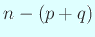 次元空間
次元空間
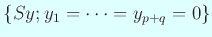 では
では 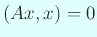 になるので、
になるので、
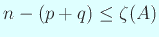 .
.
(c) から
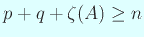 であるが、
(a) から
であるが、
(a) から
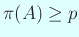 ,
(b) から
,
(b) から
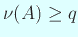 であるから、
であるから、
両端が等しいので、途中はすべて等式で 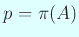 ,
, 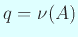 .
. 
定理 11.3 の直接的な証明が見たければ、
杉原・室田 [8] を見よ
(もちろん前項の議論から、間接的には証明は済んでいる)。




Next: 11.4 2次形式の対角化のアルゴリズム (後でどこかで使うもの)
Up: 11.3 Sylvester の慣性律の証明
Previous: 11.3.0.1 定理11.1 の証明
桂田 祐史
2015-12-22
![]() ,
,
![]() ,
,
![]() .
.
![]() は実対称行列であるから、
固有ベクトルからなる正規直交基底
は実対称行列であるから、
固有ベクトルからなる正規直交基底
![]() が存在する。
が存在する。
![]() として、
として、