| (2) | |||
| (3) |
算法の基本的な考え方は、 Householder 変換による実対称行列の三重対角化と同じである。
| (2) | |||
| (3) |
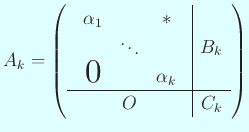
という形にすることを目指す。もしこれができれば
で、
という QR 分解が得られる。
![]() を
を
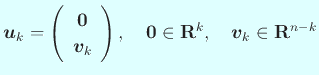
の形に取ると、
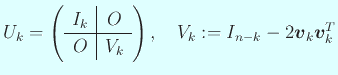
という形なるので、
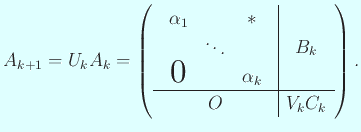
我々の目標を達成するには
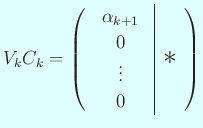
という形をしていればよい。それには、
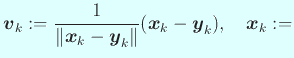
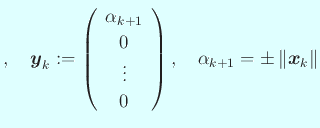
と取ればよい。
ここで ![]() となっているのは、どちらを選んでもよいが、
通常丸め誤差を抑えるために (桁落ちがおきないように)、
となっているのは、どちらを選んでもよいが、
通常丸め誤差を抑えるために (桁落ちがおきないように)、
![]() の第1成分の符号と逆になるように取るべし、
という意見がある。
次のプログラムではそうしてあるが、
その結果は MATLAB の組み込み関数である qr() の結果と一致した。
の第1成分の符号と逆になるように取るべし、
という意見がある。
次のプログラムではそうしてあるが、
その結果は MATLAB の組み込み関数である qr() の結果と一致した。
| Householder変換による QR 分解のサンプル・プログラム |
1 % qrhouse.m --- Householder 法による QR 分解 2 % 試すには n=5;a=rand(n,n);a=(a+a')/2;qr_house(a) 3 function [q,r] = qrhouse(a) 4 [n,n]=size(a); 5 U=eye(n,n); 6 for k=0:n-2 7 x=a(k+1:n,k+1); 8 alpha=-sign(x(1))*norm(x); 9 x(1)=x(1)-alpha; 10 v=x/norm(x); 11 V=eye(n-k,n-k)-2*v*v'; 12 a(k+1:n,k+1:n)=V*a(k+1:n,k+1:n); 13 U(k+1:n,:)=V*U(k+1:n,:); 14 end 15 q=U'; 16 r=a; 17 %end function |
| 実行結果 |
1 >> n=5;a=rand(n,n);a=(a+a')/2 2 a = 3 0.6273 0.7683 0.5569 0.5571 0.3849 4 0.7683 0.3716 0.4683 0.7887 0.6153 5 0.5569 0.4683 0.7764 0.6480 0.2756 6 0.5571 0.7887 0.6480 0.7036 0.3125 7 0.3849 0.6153 0.2756 0.3125 0.5668 8 >> [q r]=qrhouse(a) 9 q = 10 -0.4739 0.2935 0.1766 0.5104 -0.6306 11 -0.5804 -0.6970 0.3665 -0.2008 0.0519 12 -0.4206 -0.1361 -0.7970 0.3050 0.2764 13 -0.4209 0.4579 -0.1876 -0.7491 -0.1295 14 -0.2908 0.4470 0.4051 0.2121 0.7117 15 r = 16 -1.3238 -1.2876 -1.2151 -1.3813 -0.9518 17 0.0000 0.5390 0.1514 -0.0125 0.0431 18 0.0000 -0.0000 -0.3587 -0.1344 0.2448 19 -0.0000 0.0000 0.0000 -0.1372 0.0431 20 0.0000 0.0000 0 -0.0000 0.2283 21 >> [q2 r2]=qr(a) 22 q2 = 23 -0.4739 0.2935 0.1766 0.5104 -0.6306 24 -0.5804 -0.6970 0.3665 -0.2008 0.0519 25 -0.4206 -0.1361 -0.7970 0.3050 0.2764 26 -0.4209 0.4579 -0.1876 -0.7491 -0.1295 27 -0.2908 0.4470 0.4051 0.2121 0.7117 28 r2 = 29 -1.3238 -1.2876 -1.2151 -1.3813 -0.9518 30 0 0.5390 0.1514 -0.0125 0.0431 31 0 0 -0.3587 -0.1344 0.2448 32 0 0 0 -0.1372 0.0431 33 0 0 0 0 0.2283 34 >> norm(q-q2) 35 ans = 36 3.2522e-15 37 >> norm(r-r2) 38 ans = 39 1.2993e-15 40 >> |