Next: 3.1.2 (дҪҚзӣёзҡ„) зӣҙе’ҢгҖҒиЈңз©әй–“гҖҒе°„еҪұдҪңз”Ёзҙ гҒ§гҒӮгҒҫгӮҠжң¬гҒ«жӣёгҒ„гҒҰгҒ„гҒӘгҒ„гҒ“гҒЁ Up: 3.1 дҪҚзӣёзҡ„зӣҙе’ҢгҖҒдҪҚзӣёзҡ„иЈңз©әй–“гҒ«гҒӨгҒ„гҒҰгҒ¶гҒӨгҒ¶гҒӨ Previous: 3.1 дҪҚзӣёзҡ„зӣҙе’ҢгҖҒдҪҚзӣёзҡ„иЈңз©әй–“гҒ«гҒӨгҒ„гҒҰгҒ¶гҒӨгҒ¶гҒӨ
з·ҡеҪўд»Јж•°гғ¬гғҷгғ«гҒ®и©ұгҒ§гҒӮгӮӢгҖӮ
![\begin{jdefinition}[д»Јж•°зҡ„зӣҙе’ҢгҖҒд»Јж•°зҡ„иЈңз©әй–“]
з·ҡеһӢз©әй–“ $X$\ гҒЁ...
...гҒ®гҖҒ$Y$\ гҒҜ $Z$\ гҒ®\textbf{д»Јж•°зҡ„иЈңз©әй–“}гҒЁгҒ„гҒҶгҖӮ
\end{jdefinition}](img63.gif)
|
![\begin{jlemma}[д»Јж•°зҡ„зӣҙе’ҢгҒ«дјҙгҒҶе°„еҪұдҪңз”Ёзҙ ]
з·ҡеһӢз©әй–“ $X$\ гҒҢ $...
...
\item $P+Q=I$, $P Q=Q P=O$.
\item $P^2=P$, $Q^2=Q$.
\end{enumerate}\end{jlemma}](img65.gif)
|
иЁјжҳҺ
гҒ“гҒ®гҒЁгҒҚ
гҒЁгҒӘгӮӢгҒ®гҒ§гҖҒ
гӮ’жәҖгҒҹгҒҷ
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
гҒ“гӮҢгҒҜ
гҒЁгҒӘгӮӢгҒ®гҒ§гҖҒ
![\begin{jdefinition}[д»Јж•°зҡ„е°„еҪұдҪңз”Ёзҙ ]
з·ҡеһӢз©әй–“ $X$\ гҒҢ $Y$\ гҒЁ $Z...
...\ гҒ® $Y$\ гҒёгҒ®\textbf{д»Јж•°зҡ„е°„еҪұдҪңз”Ёзҙ }гҒЁгӮҲгҒ¶гҖӮ
\end{jdefinition}](img95.gif)
|

д»Јж•°зҡ„е°„еҪұдҪңз”Ёзҙ ![]() гҒҜ
гҒҜ ![]() гӮ’жәҖгҒҹгҒҷгӮҸгҒ‘гҒ гҒҢгҖҒ
йҖҶгҒ«гҒ“гҒ®жҖ§иіӘгӮ’жҢҒгҒӨз·ҡеһӢдҪңз”Ёзҙ гҒҢгҒӮгӮӢгҒЁгҒҚгҖҒ
дёҖгҒӨгҒ®д»Јж•°зҡ„зӣҙе’ҢеҲҶи§ЈгҒҢеҫ—гӮүгӮҢгӮӢгҒ“гҒЁгӮ’д»ҘдёӢгҒ«зӨәгҒҷгҖӮ
е…Ҳиө°гҒЈгҒҰжЁҷиӘһзҡ„гҒ«гҒҫгҒЁгӮҒгҒҰгҒҠгҒҸгҒЁгҖҒ
гӮ’жәҖгҒҹгҒҷгӮҸгҒ‘гҒ гҒҢгҖҒ
йҖҶгҒ«гҒ“гҒ®жҖ§иіӘгӮ’жҢҒгҒӨз·ҡеһӢдҪңз”Ёзҙ гҒҢгҒӮгӮӢгҒЁгҒҚгҖҒ
дёҖгҒӨгҒ®д»Јж•°зҡ„зӣҙе’ҢеҲҶи§ЈгҒҢеҫ—гӮүгӮҢгӮӢгҒ“гҒЁгӮ’д»ҘдёӢгҒ«зӨәгҒҷгҖӮ
е…Ҳиө°гҒЈгҒҰжЁҷиӘһзҡ„гҒ«гҒҫгҒЁгӮҒгҒҰгҒҠгҒҸгҒЁгҖҒ
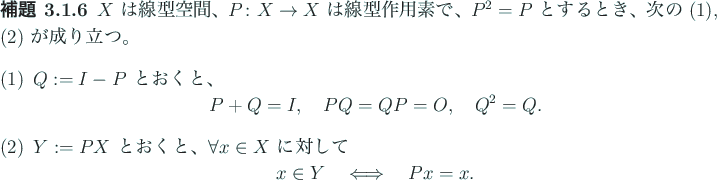
|
иЁјжҳҺ
|
|
иЁјжҳҺ
![]() гӮҲгӮҠгҖҒ
гӮҲгӮҠгҖҒ![]() . гҒҫгҒҹ
. гҒҫгҒҹ ![]() гӮҲгӮҠ
гӮҲгӮҠ
![]() гҒ§гҒӮгӮӢ
(е®ҹйҡӣ
гҒ§гҒӮгӮӢ
(е®ҹйҡӣ
![]() гҒЁгҒҷгӮӢгҒЁгҖҒ
гҒЁгҒҷгӮӢгҒЁгҖҒ![]() ,
, ![]() гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
![]() гҒЁгҒӘгӮҠгҖҒ
гҒЁгҒӘгӮҠгҖҒ
![]() гҒҢзӨәгҒ•гӮҢгӮӢ)гҖӮ
гҒҢзӨәгҒ•гӮҢгӮӢ)гҖӮ ![]()
жЎӮз”° зҘҗеҸІ