
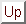


Next: B..3.0.1 符号の変化数の計算に関する注意
Up: B. Strum の方法
Previous: B..2 ユークリッドの互除法による Strum 列の生成
を実対称三重対角行列とする。
![\begin{jremark}[対称性の仮定について]\upshape
実は以下の議論�...
...�ついてくる「おまけ」ということでしょう。 \qed
\end{jremark}](img465.gif)
以下  (
(
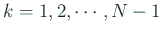 ) と仮定する。
もしある
) と仮定する。
もしある 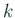 に対して
に対して 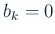 ならば
ならば
とブロック分けでき、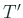 ,
, 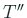 の固有値を求める問題に帰着できるから、
一般性は失われない。
の固有値を求める問題に帰着できるから、
一般性は失われない。
 を
を
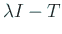 の
の 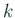 次首座小行列式とする
(
次首座小行列式とする
(
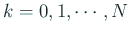 )。すなわち
)。すなわち
|
(19) |
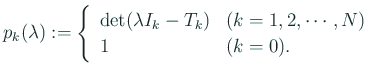 |
ただし、
すぐ分かる命題を二つ。
証明.
行列式の展開定理を用いる。


証明.
- (1)
- もしも
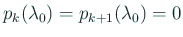 とすると、漸化式から
とすると、漸化式から
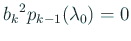 .
. 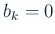 と仮定したから
と仮定したから
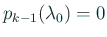 . これを繰り返すと
. これを繰り返すと
これから
これは
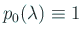 に矛盾する。
に矛盾する。
- (2)
-
 を漸化式に代入すると
を漸化式に代入すると
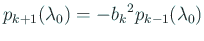 . 前項より左辺
. 前項より左辺  . これから
. これから
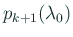 ,
,
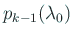 は異符号である。
は異符号である。
- (3)
-
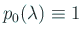 であるから明らか。
であるから明らか。
- (4)
- 漸化式
|
(20) |
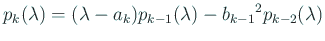 |
を微分すると、
|
(21) |
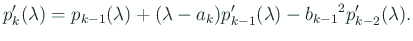 |
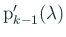 より
より
という漸化式が得られる。ここで
とおくと、漸化式は
となる。ところで
であるから、以下帰納的に
が示せる。特に
であるが、
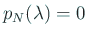 であるから
であるから

Subsections



Next: B..3.0.1 符号の変化数の計算に関する注意
Up: B. Strum の方法
Previous: B..2 ユークリッドの互除法による Strum 列の生成
桂田 祐史
2015-12-22
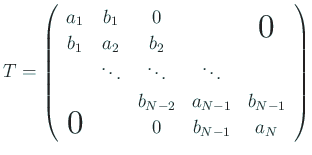
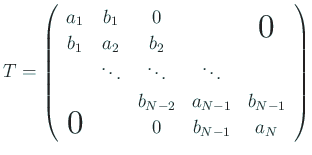
![\begin{jremark}[対称性の仮定について]\upshape
実は以下の議論�...
...�ついてくる「おまけ」ということでしょう。 \qed
\end{jremark}](img465.gif)
![]() (
(
![]() ) と仮定する。
もしある
) と仮定する。
もしある ![]() に対して
に対して ![]() ならば
ならば
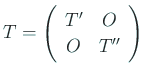
![]() を
を
![]() の
の ![]() 次首座小行列式とする
(
次首座小行列式とする
(
![]() )。すなわち
)。すなわち
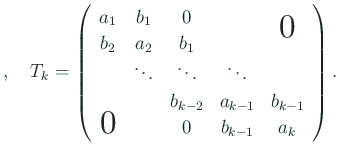
![\begin{jlemma}
% latex2html id marker 1000 [漸化式]\upshape
(\ref{eq:pkの�...
...mbda) & = & \det(\lambda I-T).
\end{array}\right.
\end{displaymath}\end{jlemma}](img467.gif)
![\begin{jlemma}
% latex2html id marker 1016 [Strum 列であること]\upshape
(...
...$\ ならば $p_N'(\lambda_0)
p_{N-1}(\lambda_0)>0$.
\end{enumerate}\end{jlemma}](img468.gif)
![]() より
より