



Next: 10 Shur 分解
Up: 9 一般化固有値問題
Previous: 9.2 Courant-Fischer の min-max
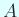 を実対称,
を実対称,  を正値対称行列とするとき、
を正値対称行列とするとき、
を満たす  ,
, 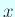 を求めよ、という一般化固有値問題を考える。
を求めよ、という一般化固有値問題を考える。
- (1)
- 固有値
 はすべて実数である。
はすべて実数である。
- (2)
 の固有値の正のものの個数
の固有値の正のものの個数
 は
は に
等しい。
に
等しい。
- (3)
- 任意に与えた実数
 に対して、
に対して、
 と
と
 分解すれば、
分解すれば、
 の対角要素のうち正, 0
, 負のものの個数が、
の対角要素のうち正, 0
, 負のものの個数が、
 より大きい、等しい、小さい固有値
より大きい、等しい、小さい固有値  の個数を与える。
の個数を与える。




Next: 10 Shur 分解
Up: 9 一般化固有値問題
Previous: 9.2 Courant-Fischer の min-max
桂田 祐史
2015-12-22
![]() を実対称,
を実対称, ![]() を正値対称行列とするとき、
を正値対称行列とするとき、