![]() に対して、
に対して、
を満たす
![]() が
が ![]() の固有値であることと、
の固有値であることと、
が
![]() が
が ![]() の固有値であるとき、
の固有値であるとき、
![]() を
固有空間 (eigenspace) と呼ぶ。
を
固有空間 (eigenspace) と呼ぶ。
![\begin{jtheorem}[固有値は固有多項式の根]\upshape
$\lambda$ が $A$\...
...-A)=0
\end{displaymath}の根であることは同値である。
\end{jtheorem}](img11.png)
|
![\begin{jdefinition}[固有多項式、固有方程式]\upshape
$p(\lambda):=\de...
...da)=0
\end{displaymath}を\textbf{固有方程式}と呼ぶ。
\end{jdefinition}](img12.png)
|
|
|
![]() の固有多項式に重根がないときはちょうど
の固有多項式に重根がないときはちょうど ![]() 個 (相異なる) 固有値が
存在することになるが、重根がある場合はその重複度分だけ同じものをならべて、
個 (相異なる) 固有値が
存在することになるが、重根がある場合はその重複度分だけ同じものをならべて、
![]() ,
, ![]() ,
, ![]() と書くことが多い。以下、
と書くことが多い。以下、
![]() 次正方行列
次正方行列 ![]() について、
について、![]() の固有値は
の固有値は ![]() ,
, ![]() ,
,
![]() である、と言ったときはそういう意味である。
例えば、
「対角行列
である、と言ったときはそういう意味である。
例えば、
「対角行列
![]() の固有値は対角成分
の固有値は対角成分 ![]() ,
, ![]() ,
,
![]() である。」…このことの証明は
である。」…このことの証明は ![]() の固有多項式についての等式
の固有多項式についての等式
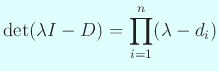
による。ちなみにこの事実は三角行列に対して一般化できる。 すなわち「
![\begin{jcorollary}[固有値は固有多項式の根ということから]\upsha...
...�� $A$ の固有値でない}.
\end{displaymath}\end{enumerate}\end{jcorollary}](img25.png)
|
|
|

|
この命題の状況のように、
![]() の固有値
の固有値 ![]() ,
, ![]() ,
, ![]() に属する
固有ベクトル
に属する
固有ベクトル ![]() ,
, ![]() ,
, ![]() が全空間の基底となるとき、
が全空間の基底となるとき、
![]() とおくと、これは非特異で
とおくと、これは非特異で
このように適当な非特異行列
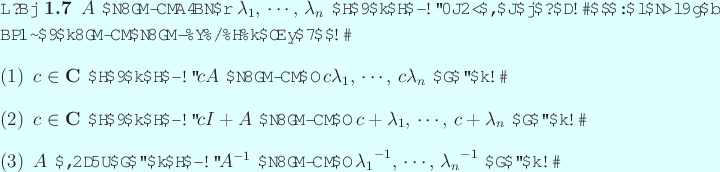
|
![]() を
を ![]() の固有値とするとき、
の固有値とするとき、
![]() は
は ![]() の固有値であるが、
その固有ベクトル
の固有値であるが、
その固有ベクトル ![]() は
は
を満たすので、
を満たす。
|
|
![\begin{jdefinition}[固有値の代数的多重度、幾何学的多重度]\upsh...
...�間 $\ker(\lambda I-A)$ の次元のことと定義する。
\end{jdefinition}](img47.png)
|