![]() сЂ«сЃЎсѓ»сЃѕсЃФтѕЌ
сЂ«сЃЎсѓ»сЃѕсЃФтѕЌ ![]() ,
, ![]() ,
, ![]() сЂї1ТгАуІгуФІсЂДсЂѓсѓІсЂесЂЇсђЂ
Gram-Schmidt сЂ«уЏ┤С║цтїќТ│ЋсђЂ
сЂцсЂЙсѓі
сЂї1ТгАуІгуФІсЂДсЂѓсѓІсЂесЂЇсђЂ
Gram-Schmidt сЂ«уЏ┤С║цтїќТ│ЋсђЂ
сЂцсЂЙсѓі ![]() ,
, ![]() ,
, ![]() ,
, ![]() сЂ«жаєсЂФ
сЂ«жаєсЂФ
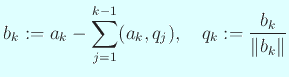 |
![]() ,
,
![]() ,
,
![]() ,
,
![]() сЂесЂісЂЈсЂесђЂ
сЂесЂісЂЈсЂесђЂ
сЂЊсЂ«тйбсЂ«тѕєУДБсЂ»СИђТёЈуџёсЂДсЂѓсѓІсђѓт«ЪжџЏ
сЂесЂЎсѓІсЂесђЂтидсЂІсѓЅ
тидУЙ║сЂ»т«ЪуЏ┤С║цУАїтѕЌсЂ«уЕЇсЂесЂЌсЂдт«ЪуЏ┤С║цУАїтѕЌ (жЋисЂЋсѓњтцЅсЂѕсЂфсЂётцЅТЈЏсЂасЂІсѓЅ) сЂДсђЂ тЈ│УЙ║сЂ»т»ЙУДњТѕљтѕєсЂїТГБсЂ«СИіСИЅУДњУАїтѕЌсЂ«уЕЇсЂесЂЌсЂдт»ЙУДњТѕљтѕєсЂїТГБсЂ«СИіСИЅУДњУАїтѕЌсЂДсЂѓсѓІсђѓ у░АтЇўсЂфУеѕу«ЌсЂДт»ЙУДњТѕљтѕєсЂїТГБсЂ«СИіСИЅУДњт«ЪуЏ┤С║цУАїтѕЌсЂ»тЇўСйЇУАїтѕЌсЂФС╗ќсЂфсѓЅсЂфсЂёсЂЊсЂесЂїтѕє сЂІсѓІсђѓ
С╗ЦСИісѓњсЂЙсЂесѓЂсЂдТгАсЂ«тЉйжАїсѓњтЙЌсѓІсђѓ
![\begin{jproposition}[QRтѕєУДБ]\upshape
$n$ ТгАТГБтЅЄУАїтѕЌ $A$ сЂФт»ЙсЂЌсЂдсђ...
...»ЙсЂЎсѓІ Gram-Schmidt сЂ«уЏ┤С║цтїќТ│ЋсЂФсѓѕсѓітЙЌсѓЅсѓїсѓІсђѓ
\end{jproposition}](img132.png)
|
(1) сЂ«тйбсЂ«тѕєУДБсѓњ QR тѕєУДБсЂетЉ╝сЂХ1сђѓ
| GramSchmidt сЂ«уЏ┤С║цтїќсЂФсѓѕсѓІ QR тѕєУДБ |
1 % GramSchmidt.m --- GramSchmidt()
2
3 % Сй┐ућеСЙІ
4 % n=3; a=rand(n,n);
5 % [q r]=GramSchmidt(a)
6 % a-q*r
7
8 % A=(a1 a2 ...,an) сЂ«тѕЌсЃЎсѓ»сЃѕсЃФсЂІсѓЅТГБУдЈуЏ┤С║цтЪ║т║Ћ
9 % q1, q2,..., qn сѓњСИдсЂ╣сЂЪ Q сѓњТ▒ѓсѓЂсѓІсђѓ
10 function [q, r] = GramSchmidt(A)
11 [n n] = size(A);
12 %
13 q=zeros(n,n);
14 r=zeros(n,n);
15 for k=1:n
16 b=A(:,k); % уггkтѕЌ a_k
17 for j=1:k-1
18 r(j,k)=q(:,j)'*A(:,k); % r_{jk} = a_k сЂе q_j сЂ«тєЁуЕЇ
19 b=b-r(j,k)*q(:,j); % b_k = a_k-(a_k,q_j)q_j
20 end
21 r(k,k)=norm(b); % r_{kk} = ||b_k||
22 q(:,k)=b/r(k,k); % q_k = b / r_{kk}
23 end
|
| GramSchmidt.m сЂ«т«ЪУАїухљТъю |
1 >> n=4;a=rand(n,n) 2 a = 3 0.9827 0.1146 0.5668 0.9616 4 0.8066 0.6649 0.8230 0.0589 5 0.7036 0.3654 0.6739 0.3603 6 0.4850 0.1400 0.9994 0.5485 7 >> [q r]=GramSchmidt(a) 8 q = 9 0.6415 -0.6491 -0.3412 -0.2251 10 0.5266 0.7307 -0.1256 -0.4160 11 0.4593 0.1624 -0.0214 0.8730 12 0.3166 -0.1355 0.9313 -0.1185 13 r = 14 1.5319 0.6358 1.4229 0.9870 15 0 0.4517 0.2074 -0.5971 16 0 0 0.6196 0.1676 17 0 0 0 0.0086 18 >> a-q*r 19 ans = 20 1.0e-15 * 21 0 0 0 0.1110 22 0 0 0 -0.0139 23 0 0 0 0 24 0.0555 0 0 0.1110 25 >> |