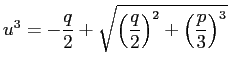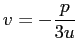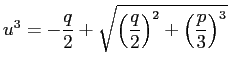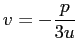

Next: 10.3 浅野雄太「正則関数の表示」
Up: 10 2005年度卒研
Previous: 10.1 どうしてまたコンピューターなのか
秋間君はハイラー・ワナーのテキストで 3 次方程式のいわゆる
「Cardano の解法」を学んだ。
これは通常のカリキュラムには含まれていなくて、
たまに解説してあっても少々舌足らずであることが少なくない
(少なくとも、
アルゴリズムの記述になっているとは到底言えない、
と感じられる解説が多い)。
複素数計算をきちんと理解して、
アルゴリズムを記述する (プログラムも書く) ことはやる価値がある、
となっての挑戦である。
レポートのタイトルそのものは 4 次方程式となったが、
3次方程式の Cardano の解法、
4次方程式の Decartes の解法10を説明し、
それをもとにしたコンピューター・プログラムを示し、
数値実験結果を載せてある。
プログラミングに詳しくない人には意外かもしれないが、
Cardano (Girolamo Cardano, 1501-1576, イタリアの Pavia にて生まれ、
Rome にて没する) の解法のプログラムが載っている本はほとんどない。
これは一つには複素数を使えるプログラミング言語が少ないためと、
3次方程式, 4次方程式は特殊で、
反復計算により一般の次数の代数方程式を解くプログラムを示すことの方が
有益だと思われているためであろう。
詳細はもちろん彼のレポートを見てもらえばよいが、
野次馬として何点か指摘しておこう。
- Cardano の時代にはまだ文字式による計算が発明されていなかったため、
Cardano は解法の説明をすべて図を使って行っていた。
- 彼にとっての数は実数であるだけでなく正の数であった。
- 有名な 4 次方程式の Ferrari の解法は説明してあるが、
あまり実用性がないとされていた。
- 虚数の導入として有名なのは、
「和が
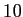 、積が
、積が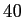 である数を求めよ」という問題であるが、
負数すらまともな数と認めない彼が虚数を考えざるを得なかったのは、
本当は3次方程式に「不還元の場合」があるのを知っていたからである。
でも不還元の場合については正直に紹介していないという。
である数を求めよ」という問題であるが、
負数すらまともな数と認めない彼が虚数を考えざるを得なかったのは、
本当は3次方程式に「不還元の場合」があるのを知っていたからである。
でも不還元の場合については正直に紹介していないという。
- 不還元の場合は、平方根、三乗根の選び方について考える必要が出て来る。
きちんと考えずに
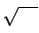 や
や
![$ \sqrt[3]{\quad}$](img174.png) などの記号と形式的な公式に
よりかかっていると、Cardano の解法を正しく理解することはできない
12。
などの記号と形式的な公式に
よりかかっていると、Cardano の解法を正しく理解することはできない
12。
- Cardano が 3次方程式の解法を Tartaglia (Nicolo Fontana Tartaglia,
1500-1557, イタリアの Brescia にて生まれ、
Venice にて没する) から公開しない約束で
教えてもらったのに著書の中に書いてしまって約束を破った
(Tartaglia の言い分)
という件については、500年近い時を隔てた、外国人である我々にはよく分からない。
Cardano 側の肩を持つ人、Tartaglia 側の肩を持つ人、両方いて、
それらの人が言うことを素直に受け入れてしまう人が多いが、
有益なこととは思えない。
少なくとも数学的な意味はない。
- Cardano は歴史上初めての「自伝」を書いたり多才な人であったようだが、
Tartaglia もユークリッドの原論やアルキメデスの著作の初めてのイタリア語への
翻訳を出版したり、
力学の議論をしたりした非凡な人物である
(ガリレオは Tartaglia の弟子に数学を学んだそうである。)。
| 不還元の場合 |
実数を係数とする 3 次方程式
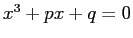 がただ一つの実根を持つ
(
がただ一つの実根を持つ
(
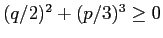 が成り立つ)
場合は Cardano の解法で特に大きな問題は生じないが、
3つの実根を持つ (
が成り立つ)
場合は Cardano の解法で特に大きな問題は生じないが、
3つの実根を持つ (
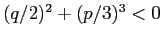 が成り立つ) 場合は、
Cardano の解法では負数の平方根と虚数の3乗根が現れてしまう。
この後者の場合を「不還元の場合」と呼ぶ。
が成り立つ) 場合は、
Cardano の解法では負数の平方根と虚数の3乗根が現れてしまう。
この後者の場合を「不還元の場合」と呼ぶ。
|
なお、秋間君は多くの人達のプログラミングの相談役となった。
彼なしでは、2005年度卒研はまったく違ったものになっていた可能性が高い。


Next: 10.3 浅野雄太「正則関数の表示」
Up: 10 2005年度卒研
Previous: 10.1 どうしてまたコンピューターなのか
桂田 祐史
2015-12-24