![]() 次正則行列
次正則行列 ![]() が
が ![]() と LU 分解されているとき、
連立1次方程式
と LU 分解されているとき、
連立1次方程式
は少ない計算量で解くことが出来る。 以下、このことを説明する。
は
という二つの問題に分解される。
まず ![]() は
は
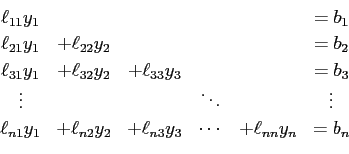
ということであり、これは上から順に
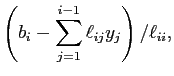 | |||
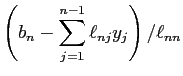 |
これを計算するには、
![]() 回の乗除算で十分である
3。
回の乗除算で十分である
3。
同様に ![]() は
は
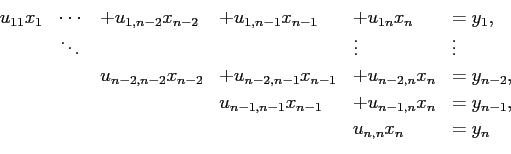
ということである。やはり
 | ||
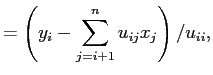 | ||
 | ||
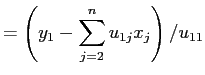 |
これも計算するには、
![]() 回の乗除算で十分である。
回の乗除算で十分である。
まとめると、
![]() 回の乗除算で連立1次方程式が解
けることになる4。
これは連立1次方程式を「普通に」解く場合に、
回の乗除算で連立1次方程式が解
けることになる4。
これは連立1次方程式を「普通に」解く場合に、
![]() に比例する回数の乗除算が必要なことと比較して、
(
に比例する回数の乗除算が必要なことと比較して、
(![]() が大きな場合は) かなり少ない回数となる。
が大きな場合は) かなり少ない回数となる。