

Next: 0.0.0.8 2.
Up: �$B2rEz�(B
Previous: �$B2rEz�(B
(1)
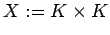 ,
,
![$ K:=\Q\cap[0,1]$](img90.png) .
.
![$ A:=[0,1]\times[0,1]$](img91.png) �$B$H$*$/$H$-!"�(B
�$B$H$*$/$H$-!"�(B
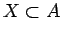 . �$B$^$?�(B
. �$B$^$?�(B 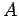 �$B$NG$0U$NJ,3d�(B
�$B$NG$0U$NJ,3d�(B 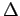 �$B$KBP$7$F!"�(B
�$BM-M}?t$NcGL)@-!"L5M}?t$NcGL)@-$+$i�(B
�$B$KBP$7$F!"�(B
�$BM-M}?t$NcGL)@-!"L5M}?t$NcGL)@-$+$i�(B
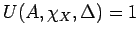 ,
,
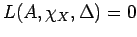 �$B$G$"$k$N$G!"�(B
�$B$G$"$k$N$G!"�(B
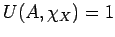 ,
,
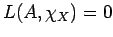 . �$B$f$($K�(B
. �$B$f$($K�(B 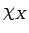 �$B$O�(B
�$B$O�(B 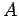 �$B$G@QJ,2DG=$G$J$$!#�(B
�$B$9$J$o$A�(B
�$B$G@QJ,2DG=$G$J$$!#�(B
�$B$9$J$o$A�(B 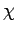 �$B$O�(BJordan�$B2DB,$G$O$J$$!#�(B
(2)
�$B$O�(BJordan�$B2DB,$G$O$J$$!#�(B
(2) 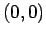 ,
, 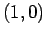 ,
, 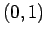 �$B$rD:E@$H$9$k;03Q7A�(B (�$B<~$*$h$SFbIt�(B) �$B$r�(B
�$B$rD:E@$H$9$k;03Q7A�(B (�$B<~$*$h$SFbIt�(B) �$B$r�(B 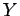 �$B$H$9$k$H!"�(B
�$B$H$9$k$H!"�(B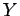 �$B$O5a$a$k>r7o$rK~$?$9!#�(B �$BFC$K!"�(B
�$B$O5a$a$k>r7o$rK~$?$9!#�(B �$BFC$K!"�(B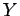 �$B$N6-3&$OM-3&JD6h4V>e$N�(B
�$BO"B34X?t$N%0%i%UM-8B8D$+$i$J$k$3$H$+$i!"�(B
�$B$N6-3&$OM-3&JD6h4V>e$N�(B
�$BO"B34X?t$N%0%i%UM-8B8D$+$i$J$k$3$H$+$i!"�(B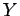 �$B$,�(B Jordan �$B2DB,$G$"$k$3$H$,�(B
�$BJ,$+$k!#�(B
�$B$,�(B Jordan �$B2DB,$G$"$k$3$H$,�(B
�$BJ,$+$k!#�(B 
ARRAY(0xed5784)


Next: 0.0.0.8 2.
Up: �$B2rEz�(B
Previous: �$B2rEz�(B
Masashi Katsurada
�$BJ?@.�(B20�$BG/�(B2�$B7n�(B12�$BF|�(B