以下紹介する命題の証明は、桂田 [6] で読める。
![]() は自然に
は自然に ![]() 上のベクトル空間であるが、
任意の
上のベクトル空間であるが、
任意の
![]() に対して
に対して
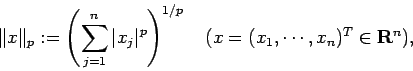
実数を成分とする ![]() 行
行 ![]() 列の
行列全体の集合
を
列の
行列全体の集合
を
![]() と書く。
と書く。
![]() ならば
ならば
![]() は多元環、
は多元環、
![]() であっても
であっても
![]() はベクトル空間の構造を持つ。
はベクトル空間の構造を持つ。
![]() は線型写像
は線型写像
![]() を引き
起こすが、
を引き
起こすが、![]() の任意のノルム
の任意のノルム ![]() ,
, ![]() の任意のノルム
の任意のノルム
![]() に対して、
に対して、
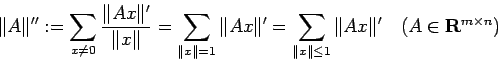
任意の
![]() に対して、
に対して、
![]() のスペクトル半径 (
のスペクトル半径 (![]() の固有値の絶対値の最大値) を
の固有値の絶対値の最大値) を ![]() と書く。
と書く。
![\begin{jlemma}[作用素ノルム≧スペクトル半径]
$\Vert\cdot\Vert$ �...
...\Vert\ge r(A)\quad
\mbox{($A\in\R^{n\times n}$)}.
\end{displaymath}\end{jlemma}](img108.png)
|
![]() に
に ![]() ノルムを与えたとき、
ノルムを与えたとき、
![]() の作用素ノルム
の作用素ノルム
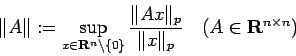
![\begin{jproposition}[行列の $p$ ノルム]
任意の $n\in\N$, $A=(a_{ij})\...
...$A$ が正規行列
($A A^T=A^T A$) ならばなりたつ。
\end{jproposition}](img111.png)
|