

Next: を計算で求めるのが楽であること
Up: 4 Lanczos 法
Previous: Lanczos 法の利点
必要ならばシフトを行う。
すなわち任意に選んだ
 に対して、
に対して、
そこで
とおくと
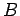 の Cholesky 分解を
の Cholesky 分解を
として、上の式に代入すると
左から
 をかけると
(ただし
をかけると
(ただし
 )
)
そこで
とおくと、
という標準固有値問題に帰着された。
これに Lanczos 法を適用して、対称三重対角行列 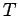 の
固有値問題
の
固有値問題
に変換する。


Next: を計算で求めるのが楽であること
Up: 4 Lanczos 法
Previous: Lanczos 法の利点
桂田 祐史
2014-05-27
![]() の Cholesky 分解を
の Cholesky 分解を
![]() の
固有値問題
の
固有値問題