2.1 相似変換

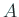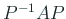固有値問題でもっとも基本的な方法は相似変換である。これは行列 $A$ を正則行列 $P$ によって、$P^{-1}A P$ に変換することを意味する。

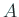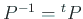に注意しよう。$A$ が実対称な場合には $P$ として実直交行列が使われる。 この場合 $P^{-1}={}^t P$ であり、計算が簡単になることの他に、様々な利点 がある。

実対称行列の、実直交行列による相似変換は実対称行列である:

$$(P^T A P)^T=P^T A^T (P^T)^T=P^T A P.$$

実直交行列による変換として、次の三つが重要である。

(1)

Givens 変換 -- 2 次元平面における回転

(2)

鏡映変換 (Householder 変換) -- 超平面に関する対称移動

(3)

QR 変換