


Next: 1.1.0.2 特異値問題
Up: 1.1 問題の定式化
Previous: 1.1 問題の定式化
行列 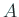 ,
, 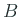 が与えられた時、方程式
が与えられた時、方程式
を満たすスカラー 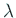 , ベクトル
, ベクトル 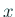 を求める問題を一般化固有値問
題という。これは
を求める問題を一般化固有値問
題という。これは 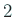 次形式の固有値問題などに関係して現れる。
次形式の固有値問題などに関係して現れる。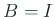 (単位行列) の場合は通常の固有値問題になる。
応用上は
(単位行列) の場合は通常の固有値問題になる。
応用上は 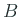 は多くの場合、正定値対称行列になる。
は多くの場合、正定値対称行列になる。
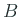 が正則である場合、上の方程式に
が正則である場合、上の方程式に 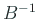 をかけて
をかけて
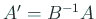 とおくと
とおくと
となって、形式的には通常の固有値問題に帰着するが、
このやり方は大抵の場合、
得策ではない (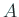 ,
, 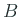 が対称であっても、
が対称であっても、
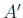 が対称であるとは限らなくなるなどの理由がある)。
簡単なことは次の文書に書いておいた。
が対称であるとは限らなくなるなどの理由がある)。
簡単なことは次の文書に書いておいた。
『一般化固有値問題メモ』
http://nalab.mind.meiji.ac.jp/~mk/labo/text/generalized-eigenvalue-problem.pdf



Next: 1.1.0.2 特異値問題
Up: 1.1 問題の定式化
Previous: 1.1 問題の定式化
桂田 祐史
2015-12-22