![]() が対角化可能としておく (これは余計な仮定か?)。
つまり、
が対角化可能としておく (これは余計な仮定か?)。
つまり、![]() に属する固有ベクトル
に属する固有ベクトル ![]() が存在し、
が存在し、
![]() ,
, ![]() ,
, ![]() が基底となると仮定する。
が基底となると仮定する。
よく知られているように、
![]() は、
は、
![]() の Hermite 共役
の Hermite 共役 ![]() の固有値になるが、
その固有ベクトル
の固有値になるが、
その固有ベクトル ![]() をシフト法で求めておく
(もちろん
をシフト法で求めておく
(もちろん ![]() が「対称」ならば
が「対称」ならば
![]() で、
で、
![]() と取れるので、対称の場合にやった操作の一般化になっている)。
と取れるので、対称の場合にやった操作の一般化になっている)。
必要ならば定数倍することによって、
![]() となるようにできる。実際、
となるようにできる。実際、
![]() に注意して、
に注意して、
であるから、
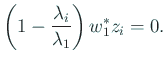
ゆえに
一方
そこで
![]() とおくと、
とおくと、
また
ゆえに ![]() について冪乗法を適用すると、
について冪乗法を適用すると、![]() が得られる。
が得られる。