


Next: 2.7 Wielandt の減次
Up: 2 解法についての概観
Previous: 2.5.0.1 計算上の注意:
既に得られている近似固有値の精度を改良したい、あるいは、ある指定した
値に最も近い固有値を求める方法である。
行列 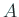 の固有値
の固有値 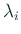 に対する近似固有値
に対する近似固有値
 が分かっ
ているとしよう。この時、
が分かっ
ているとしよう。この時、
の固有値は
となる。
 は
は 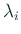 の近似値ということで、絶対値が最小
なのは
の近似値ということで、絶対値が最小
なのは
 であると期待できる。よって、
であると期待できる。よって、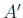 に対し
て逆反復法を適用すれば、この値(それを
に対し
て逆反復法を適用すれば、この値(それを
 とおこう)が高精
度に計算できる。こうして
とおこう)が高精
度に計算できる。こうして
により 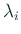 が求まる。
が求まる。



Next: 2.7 Wielandt の減次
Up: 2 解法についての概観
Previous: 2.5.0.1 計算上の注意:
桂田 祐史
2015-12-22
![]() の固有値
の固有値 ![]() に対する近似固有値
に対する近似固有値
![]() が分かっ
ているとしよう。この時、
が分かっ
ているとしよう。この時、