Next: A..3 Bessel 関数の性質 Up: A..2 Bessel の微分方程式 Previous: A..2.2 Frobenius の方法で解を求める
![]() であるとき、
であるとき、
![]() ,
,
![]() は1次独立である
(したがって (3) の解の基本系になる)。
これは両者の級数表示を見て、
は1次独立である
(したがって (3) の解の基本系になる)。
これは両者の級数表示を見て、
![]() のときの増大度を考えても容易に証明できるが、
次の補題からも分かる。
のときの増大度を考えても容易に証明できるが、
次の補題からも分かる。

|

ロンスキアンの等式から想像できることだが、
![]() のとき
のとき ![]() ,
,
![]() は1次従属になる。
これは容易に確かめられる関係
は1次従属になる。
これは容易に確かめられる関係
から明らかである。
さて、
いよいよ第二種ベッセル関数 (ノイマン関数ともいう) ![]() を導入しよう。
を導入しよう。
まず
![]() の場合に
の場合に
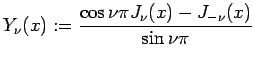
とおく。 これは
さらに ![]() に対して広義一様収束極限
に対して広義一様収束極限
が存在する。そこで
とおくと、 これも (3) の解であるが、 (5) より8
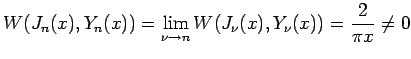
であるから、
以上をまとめると次の定理が得られる。
|
|
桂田 祐史